あなたはオイラーの等式を知ってますか？

2020年8月18日

これがオイラーの等式(Euler’s identity)です。

不思議ですよね？　e（ネイピアの数）は、2.71828182846…であり、π（円周率）は、3.14159265359…であるにもかかわらず、eを、（i（虚数）×π）乗をすると－１になるなんて、信じられますか？

そりゃ、オイラーの公式

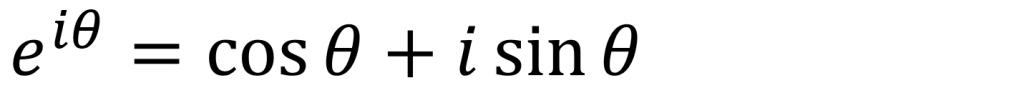
を覚えて、θ＝πとおけば、－1になるくらいはすぐわかりますけれどもね。無理数の無理数乗それも虚数乗して、－１になるなんて、まさに、何だこりゃ～です(@_@。

この公式の証明はいくつかあって、Wikipediaの説明が次のURLにあります。