整数と素数の関係を複素数に発展したらリーマン予想の問題に至る~なんのこっちゃ( ゚Д゚)
こんな式があります。
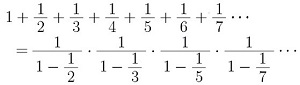
左辺は、全自然数の逆数の総和、右辺は、すべての素数が登場する多項式の無限積(オイラー積)です。
リーマンはこの式を複素数に拡張して「ゼータ(ζ)関数」と名付け(上記式は、ゼータ関数ζ(s)のs=1の場合です)、『 ζ(s)=0となるような複素数sは、実質的には実数の部分が1/2になるものしかない』、と予想したそうです(これが、リーマン予想)。
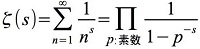
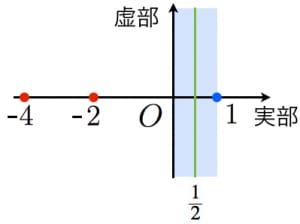
これが証明できれば、ある数以下の素数はおよそ何個あるか定式化できることにつながるとのことです。
このリーマン予想も、ミレニアム懸賞問題のうちのひとつです(2020年6月17日の当ブログには、ミレニアム懸賞問題の他の一つのNavier–Stokes 方程式があげられています)。
分かりやすい解説は、次のURLをご参照ください。