黄金比の表現はこんなにもあったのです( ﾟДﾟ)

2020年11月10日

長方形は縦と横の長さの比が黄金比になるとき、安定した美感を与えるという説があり、長方形の形状の物の縦横比に利用されることが多く、名刺をはじめとする様々なカード類などがそうなっているらしい。本Blogのフィボナッチ数列の説明のとき（2020年8月26日）、この値は出てきております。

具体的には、方程式ｘ^２-ｘ－１＝0（式①）の解の一つです。

$\phi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\cdots$

ところで、この数は、無限連分数表示や、

無限多重平方根表示もできるとか　(^_-)-☆

ちなみに、無限連分数表記は、方程式①を

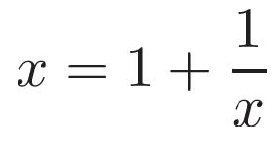
と変形すれば、理解できますし、無限多重平方根表示は、方程式①を

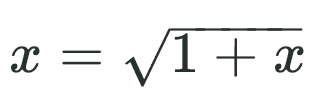
と変形すれば理解できす。

参考文献は次の通りです：