文庫版の「算法少女」 (ちくま学芸文庫)に次のような問題が載っています。

所謂、円周率(π)を求める問題です。やってみました!
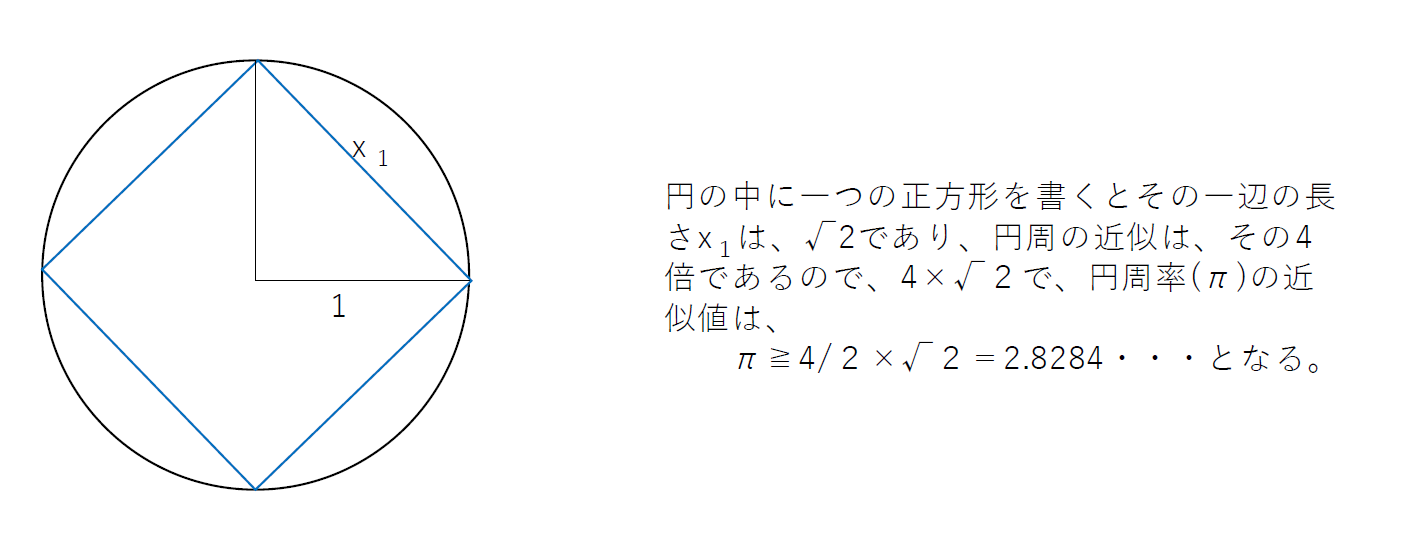
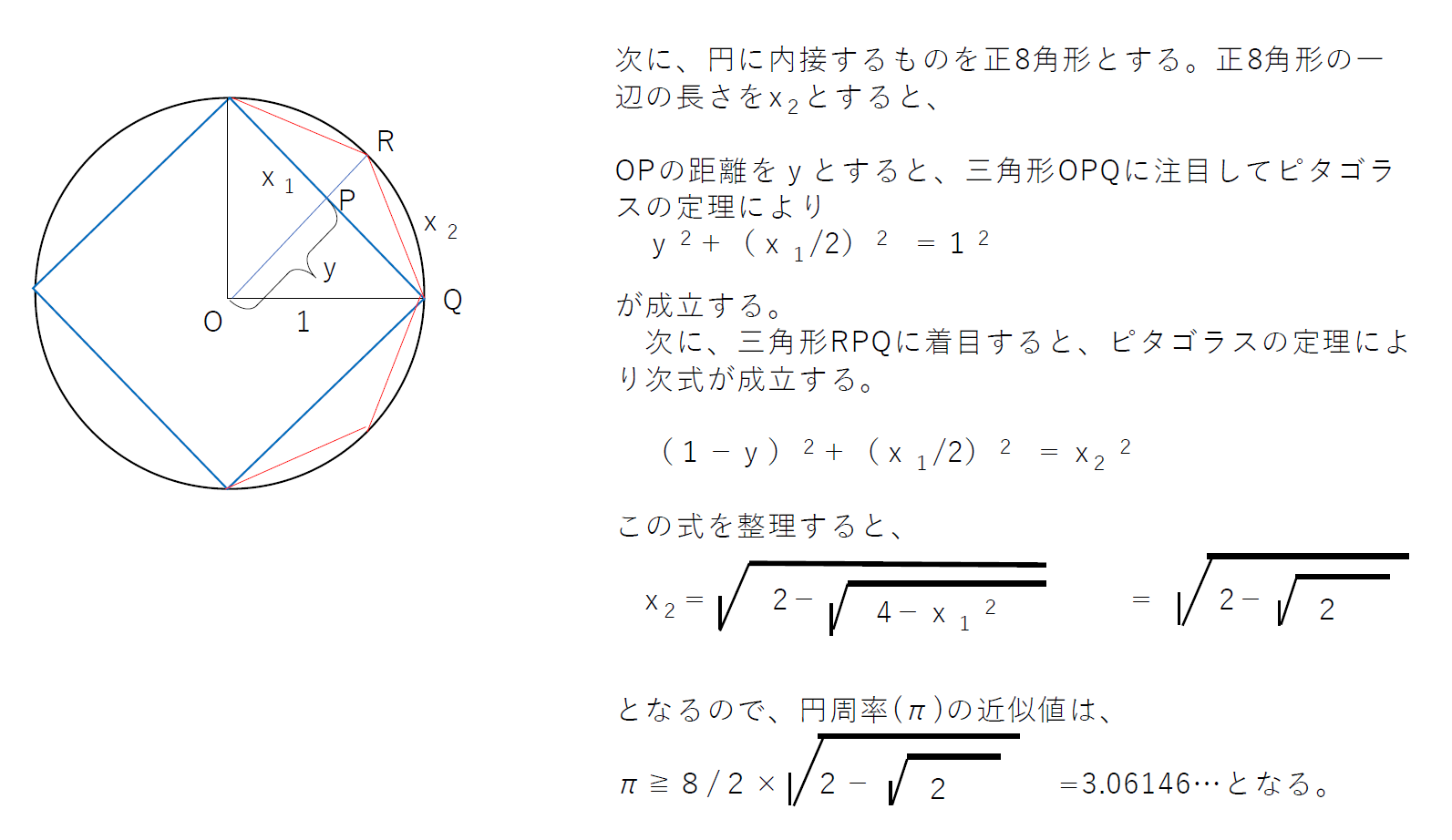
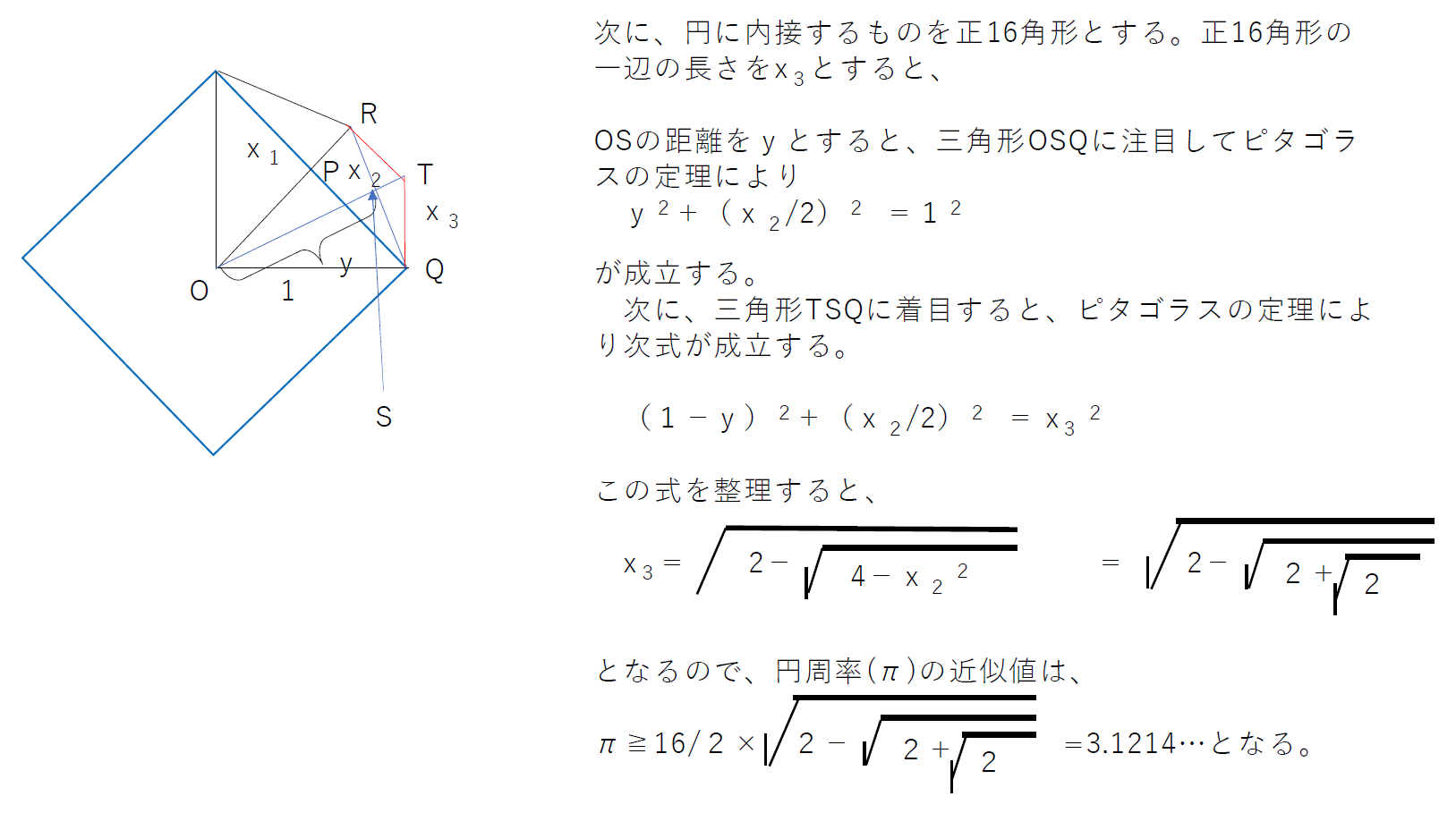
このように次々と内接する多角形について求めてゆけば良いのですが、ここまでで、円周率は、xiの漸化式になることが分かります。そこで、これまでの関係から、次のような計算結果が求まります。
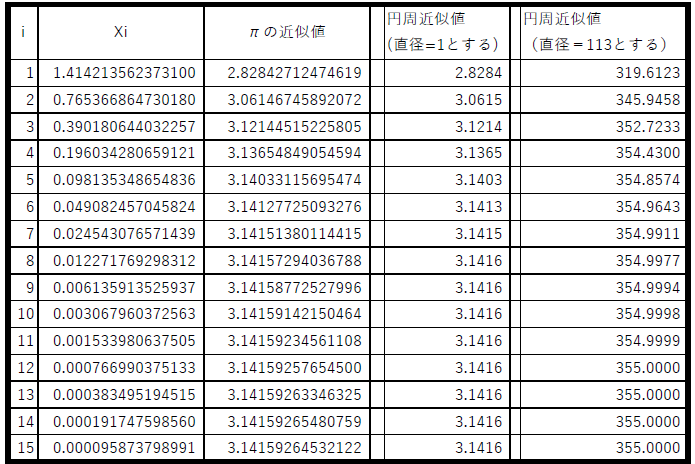
そして、直径を113にすると、円周が355となることもわかります。つまり、πの近似値は、113/355=3.14159292となります(πの真値は、π = 3.14159 26535 89793 23846 26433 83279 50288 …です)。
この問題は、とても勉強になりました(^_-)-☆ ああ、シンド!!
最後に、検算をしてみました。単位円に内接する正多角形の外周の長さは、次の計算で求まります。
L=sin (π/2^(i+1) ) × 2^(i+1) (^はべき乗を表す)
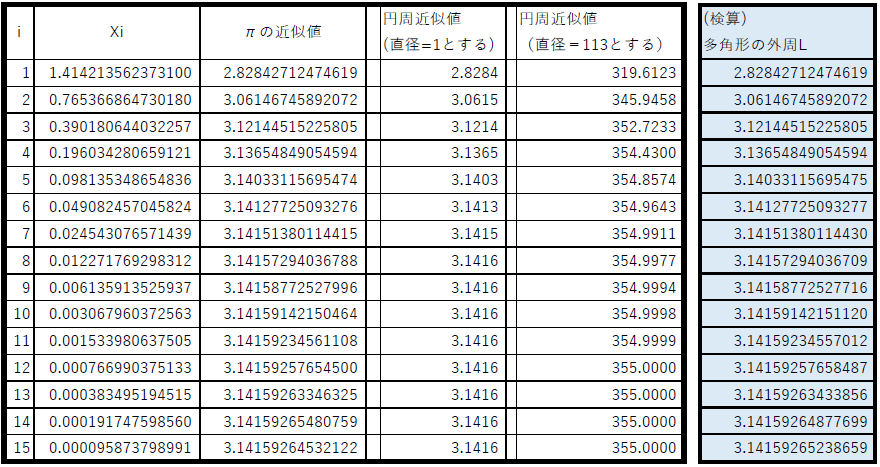
検算の方は、どんどんπの真値に向かっていきますが、多角形の計算でおこなった方は、i=7(正512角形)あたりで計算誤差が生じております。 ム?これはエクセルの問題か??