文庫版の「算法少女」 (ちくま学芸文庫)の190-191頁に次のような円周率の式が載っています。
いったいこの式はどうやって導かれたのかを、探してみたところ、ニュートンがテイラー展開をつかって求めたものに相当することが分かりました。具体的には、たとえばarcsin(sinの逆関数)を展開して求めます。
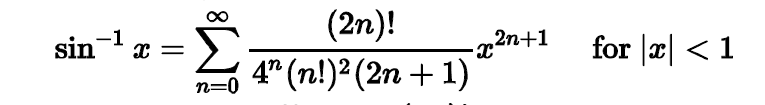
なお、この式は、Wikipediaにも掲載されております。
https://ja.wikipedia.org/wiki/%E3%83%86%E3%82%A4%E3%83%A9%E3%83%BC%E5%B1%95%E9%96%8B
上式をもう少しわかり易く書き下すと、
arcsinX=x+ 1/6×(x^3) + 3/40×(x^5)+ 5/112×(x^7) …
(^はべき乗表記)となり、sin(π/6)=1/2 ですから、arcsin(1/2)=π/6 であり、上式においてx=1/2 を入れて、6倍するとお目当てのπが求まります。この式と「算法少女」の本の式は同じです。
πの式の初項は、6×1/2=3、2項は、6×1/6×(1/2)^3=1/8、3項は、6×3/40×(1/2)^7=9/640となり、4項は、6×5/112×(1/2)^7=15/7168、・・・以下求まります。次表をみてください。
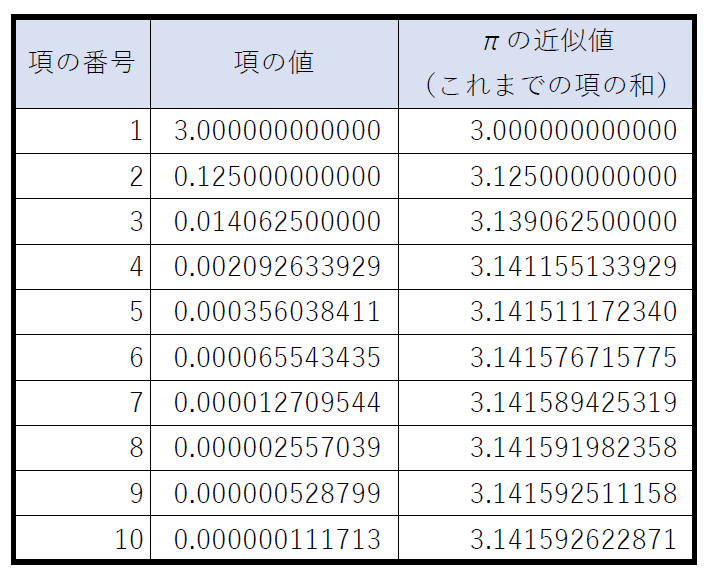
このように、この算法少女の時代(江戸時代)に、西洋では微分積分の力を借りて、πを求めていたことが分かりました。
・・・・ しかし、arcsinって、なんだったっけと、大学の関数論で習ったことを完全に忘却しているこの私の学力低下は、一体どういうことでしょうかね~!?
