先のビー玉の動きのお話(2022年7月6日)で、ちょっとスッキリしていなかったのは、ビー玉は、滑っているのか、転がっているのか、はたまた滑りながら転がっているのか、という点だったのですが、次のサイトを見つけました。
「水平面上の球体のすべりと転がり」
https://yokkun831.hatenablog.com/entry/2020/02/07/154255
そこで、もう一度、考え直してみることにしました。
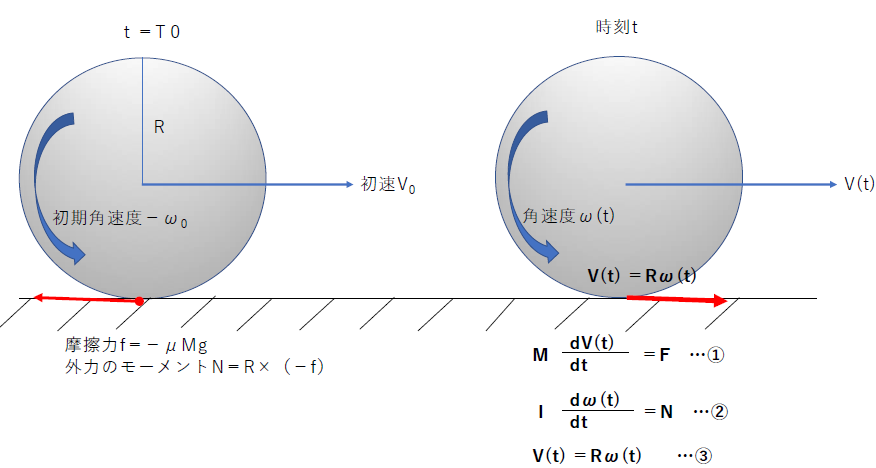
ビー玉にバックスピンをかけて時刻T0でスタートして、時刻tのときの運動を考えるときに、動摩擦係数をμとして、重心の運動方程式は、①が成立し、具体的には、次の式が成立します。この場合、運動は図の右方向を正とします。つまり、この動摩擦力が働くということは、滑っている(あるいは滑りながら回転していることを意味します)。滑らず回転するだけなら、静止摩擦力が働くということです。
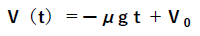
また、重心の周りの回転の運動方程式②が成立し、具体的には次の式が成立します。この場合、回転は時計方向を正とします。
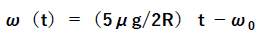
転がっているときに成立する式は③です。
そこで、夫々がゼロとなる時刻を計算します。
式①から得られたV(t)=0となるのは、T1=V0/(μg)であり、式②から得られたω(t)=0となるのは、T2=2Rω0/(5μg)であります。
そして、式③が成立するT3は、T3=2(v0+Rω0)/(7μg)となります。
ビー玉が完全に停止するT1=T2の条件は、V0=2Rω0/5です。このとき、T3=T1=T2=2Rω0/(5μg)となります。
従って、条件分けをしますと、
(ⅰ)v0<2Rω0/5のとき、T1<T2<T3が成立し、
t=T1で重心速度が0となり、逆行をはじめ、t=T2で角速度が0となることを経由して、T=T3で滑りから転がり(反時計回り)へ移行する。
(ⅱ)v0=2Rω0/5のとき、t=T1=T2=T3=2Rω0/(5μg)で滑ってきたビー玉は静止する。
(ⅲ)v0>2Rω0/5のとき、T2<T1<T3が成立し、
t=T2で角速度が0となり、その後T1で逆走をはじめ、T=T3で滑りから転がり(反時計回り)へ移行する。
ムム、また深みにはまってしまった! どうも頭がすっきりしないのは、暑さのせいだけではないような気がします。