ビー玉のバックスピンの問題は、なかなか奥が深いのですが色々調べていると、玉突き(ビリヤード)でもバックスピンの話があるようです。しかし見つけた阪大理学部物理学科の大学院の入試問題2016年の問題1は、逆走までの問題ではありませんでした。次のサイトにあります。
https://www.phys.sci.osaka-u.ac.jp/ja/grad/pdf/kakomondai/physics2016.pdf
ちょっと気になったので、解いてみることにしました。
まずは、問題(1)と(2)からです。


さて、以下回答ですが、(a)はこれまでも算出していますが、今回は力まかせに答えを求めてみます。


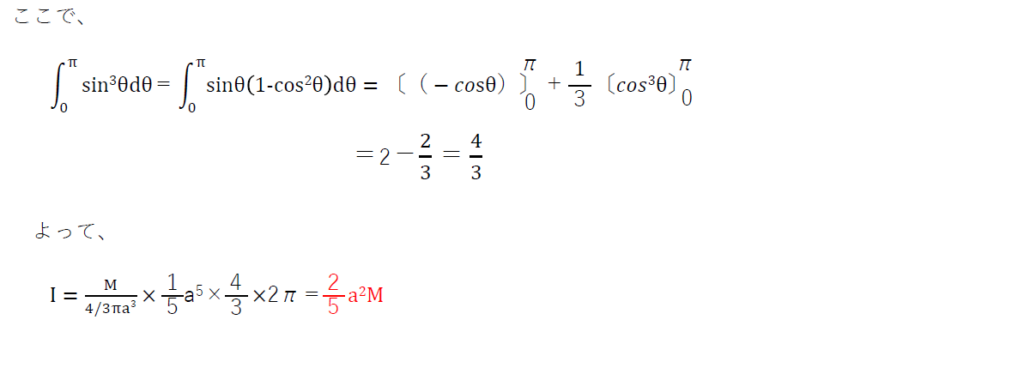
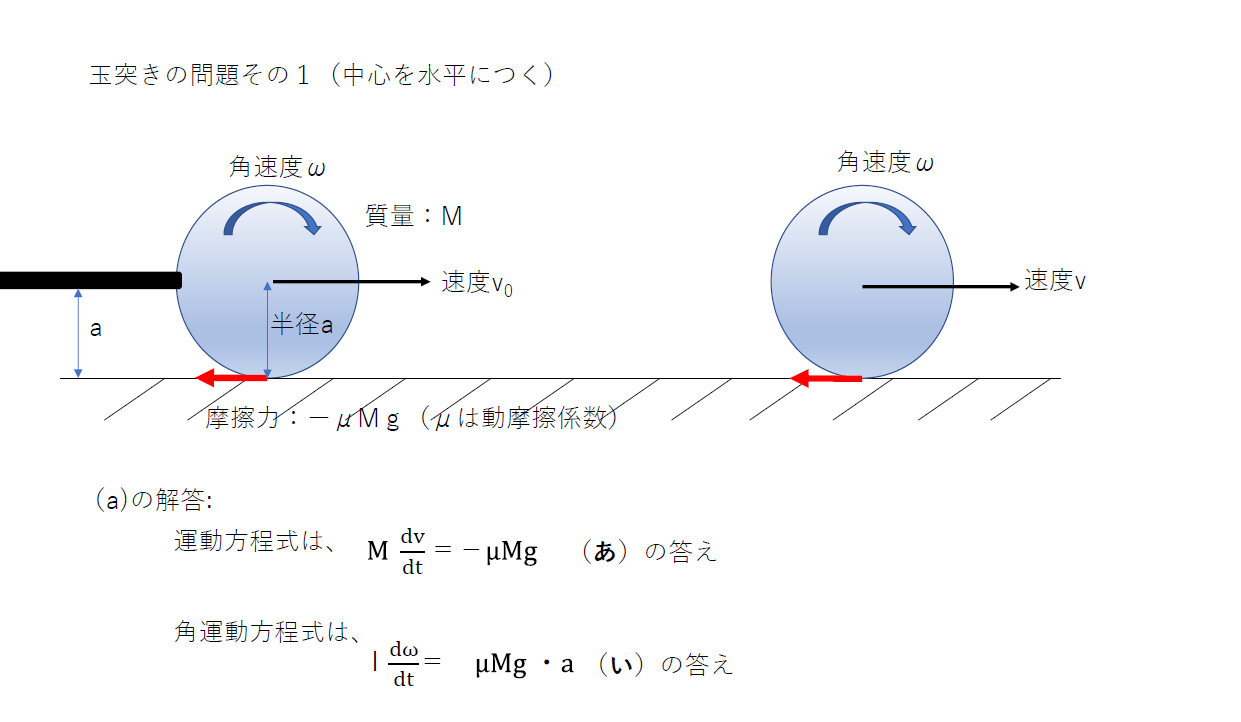
つぎに、(2)の(a)の回答です。球はt=0で回転をはじめ、t≦Tまでは、滑りながら前進するということです。
続けて、(b)、(c)の答えを求めます。

次に、(d)の答えなのですが、t>Tとなると、球は滑らず回転しているので、v=aωが成立します。ということは、v=5/7voであり、ω=5/7・(v0/a)となります。 このままどこまでも回転し、この球は定速度で進んでゆくことになることを示しています。
次に(e)の答えです。


ということで、本来、(e)の2つの答えはピッタンコあいました。めでたしめでたし。球の重心の速度v(t)と、球の床との接点の速度u(t)が異なることが面白いです!!
なお、本問題は、(3)、(4)の続きの問題がありますので、そちらはまた解けたら、本サイトにアップします。