またしても鈴木貫太郎先生の問題(^-^;
鈴木貫太郎先生が次の問題を出していました。鈴木先生は華麗に解いてましたが、私は泥臭く解きました。
三次方程式の解に関するナイスな問題
https://www.youtube.com/watch?v=DBFgASHNsys&t=1s
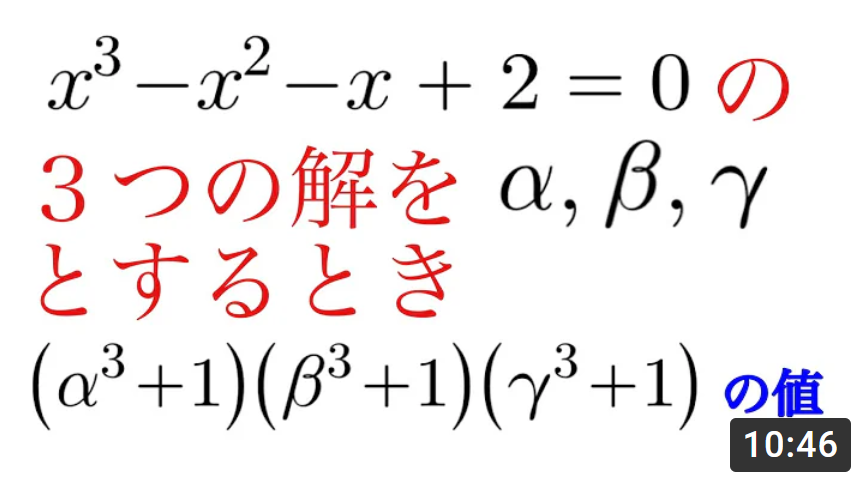
与えられた式から、α3+1=α2+α-1、β3+1=β2+β-1、γ3+1=γ2+γ-1であるので、
X=(α3+1)(β3+1)(γ3+1)
=(α2+α-1)(β2+β-1)(γ2+γ-1)
=αβγ{αβγ+(αβ+βγ+γα)+(α+β+γ)+1}ーαβ(αβ+α+β+1)ーβγ(βγ+β+γ+1)-γα(γα+γ+α+1)+(α2+β2+γ2)+(α+β+γ)ー1
Y=ーαβ(αβ+α+β+1)ーβγ(βγ+β+γ+1)-γα(γα+γ+α+1)とおくと、
Y=ー(α2β2+β2γ2+γ2α2)ー(α2β+β2α+β2γ+γ2β+γ2α+α2γ)-(αβ+βα+γα)となる。
ここで、3次方程式の係数と解の関係から、α+β+γ=1、αβ+βα+γα=-1、αβγ=-2は既知であり、解っていないのは、α2+β2+γ2と、α2β2+β2γ2+γ2α2と、α2β+β2α+β2γ+γ2β+γ2α+α2γであるが、これは、次のようにして求められます。
(α+β+γ)2=α2+β2+γ2+2(αβ+βγ+γα)=1であるから、α2+β2+γ2=1-2(-1)=3となり、
(αβ+βα+γα)2=α2β2+β2γ2+γ2α2+2αβγ(α+β+γ)=1であるから、α2β2+β2γ2+γ2α2+2(-2)(1)=1より、α2β2+β2γ2+γ2α2=5となります。
また、(α+β+γ)(αβ+βα+γα)=α2β+β2α+β2γ+γ2β+γ2α+α2γ+3αβγ=-1であるから、α2β+β2α+β2γ+γ2β+γ2α+α2γ=-1-3(-2)=5となります。
従って、Y=-5-5-(-1)=-9
よって、 X=αβγ{αβγ+(αβ+βγ+γα)+(α+β+γ)+1}+Y+(α2+β2+γ2)+(α+β+γ)ー1
=(-2){(-2)+(-1)+1+1}-9+3+1-1=-4
答えは鈴木貫太郎先生のものとあってます!!
ということで、華麗ではなく、力任せの解き方でした!大変失礼をば。
今度時間見つけて別の解き方にチャレンジします (^_-)-☆