そもそも、鈴木貫太郎先生はどう解いたのか?
先(2022年8月29日記事)に次の問題を力まかせに解きましたが、スマートな解き方はどうであったのか、YouTubeを見て考えました。
https://www.youtube.com/watch?v=DBFgASHNsys&t=1s
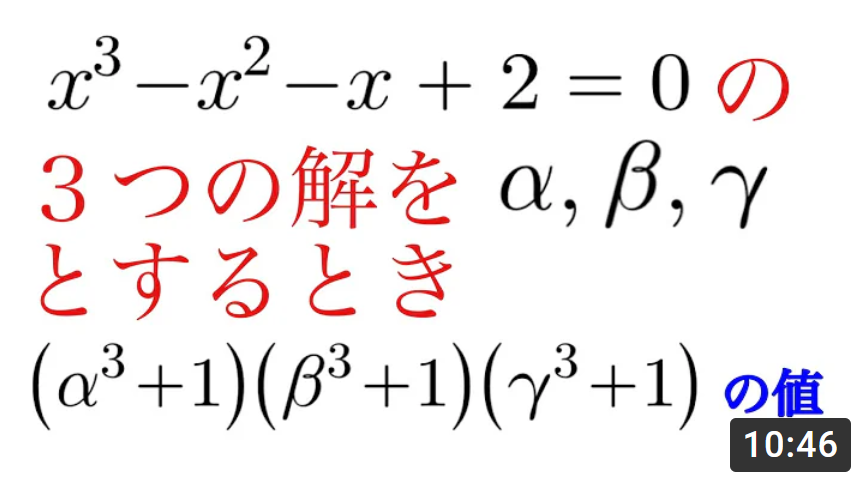
X=(α3+1)(β3+1)(γ3+1)=(α+1)(α2-α+1)(β+1)(β2-β+1)(γ+1)(γ2-γ+1)=(α+1)(β+1)(γ+1)(α2-α+1)(β2-β+1)(γ2-γ+1)と式変形をします。
次に、x2-x+1=0の方程式の解を考えます。このあたりが、鈴木貫太郎先生の凄いところです。
この式の解は、x=(1±√3i)/2となりますが、これを極座標で描くと次のZとZ5に相当します。
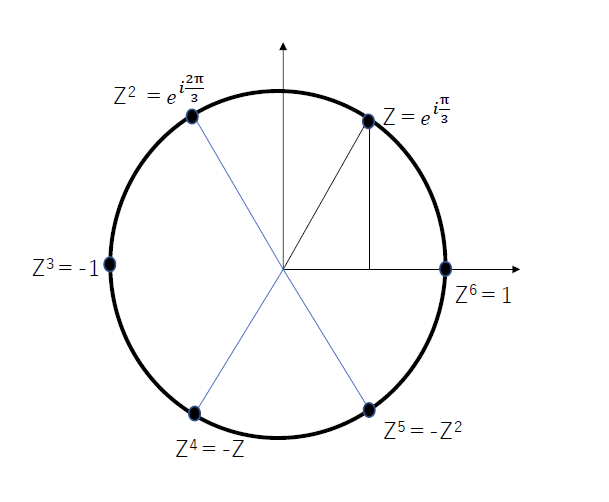
そして、X=(α+1)(β+1)(γ+1)(α2-α+1)(β2-β+1)(γ2-γ+1)=(α+1)(β+1)(γ+1)(α2-α+1)(β2-β+1)(γ2-γ+1)=(α+1)(β+1)(γ+1)(α-Z)(α-z5)(β-Z)(β-z5)(γ-Z)(γ-z5)となります。
そして、Y=x3-x2-x+2=(x-α)(x-β)(x-γ)という式が成立しますから、x=-1を入れると
-1=(-1-α)(-1-β)(-1-γ)となり、上式の (α+1)(β+1)(γ+1)=-1となります。
次に、式Yにおいて、x=Zを入力すると、Y=z3-z2-z+2=(z-α)(z-β)(z-γ)が成立し、
-1-z2-z+2=(z-α)(z-β)(z-γ) となり、(z-α)(z-β)(z-γ)=-1-(z-1)-z+2=2-2z
また、式Yにおいて、x=Z5を入力すると、(Z5)3-(Z5)2-(z5)+2=(Z5-α)(Z5-β)(Z5-γ)であるが、式変形すると、(Z5-α)(Z5-β)(Z5-γ)=-1-(z5-1)-z5+2=2-2Z5=2-2(-z2)=2(1+Z2 )=2z
よって、X=(-1)‣(2-2z)2z=4(z2-z)=-4となります。
以上で、おしまいです。こちらの解法がスマートですね~ (^_-)-☆