不思議な三角形!?

こんな問題を出されました。
下の左の図形の三角形!?を①～④の図形に切り分け、並べなおすと1マス増えた右の三角形!?になります。

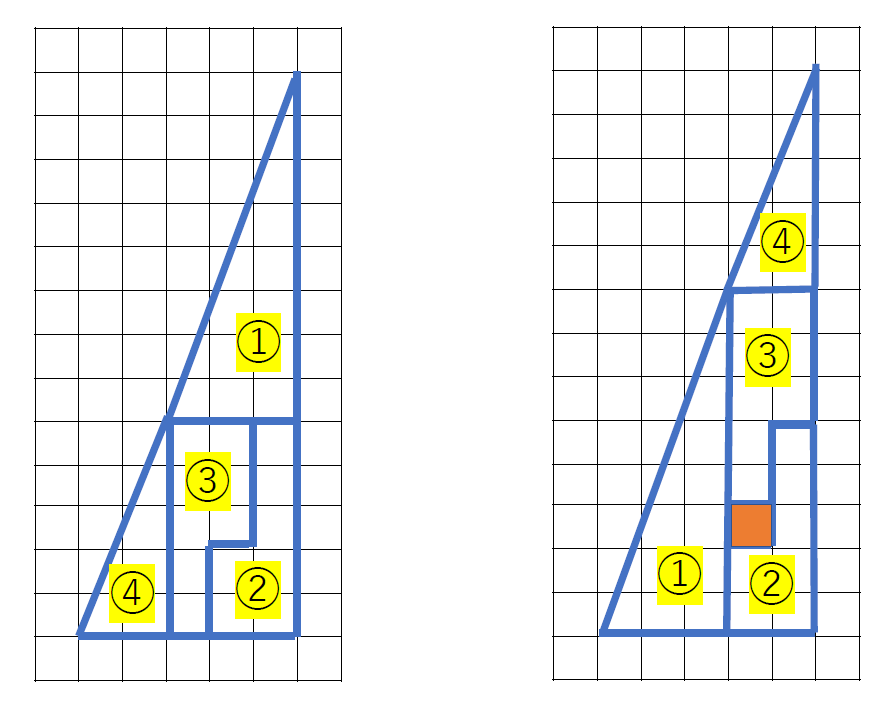
あら？？？　わかりますか？

これはもともとの左の三角形!?は、実は、三角形ではなかったのですね。④の三角形は、底辺が２、高さが５なのですが、①の三角形は実は底辺が３で高さは８なので、相似形ではありません（相似形に①の三角形をするには底辺が３なら、高さは７．５でないといけないのです）。
なお、方眼紙のマス目の長さは１とします。

ですから、最初の図形も、次の図形も三角形ではなく実は四角形ですね。　

ちなみに、最初の左の四角形の面積は、
①の面積＋②の面積＋③の面積＋④の面積＝（３×８÷２）＋７＋８＋（２×５÷２）＝３２

次の右の四角形の面積は、①＋②＋③＋④＋１（増えた1マス）＝３３で、①の違いがあります。これは、次の赤色の補助線を引くとよくわかります。
赤の線を斜辺とする三角形の面積は、５×１３÷２＝３２．５です。

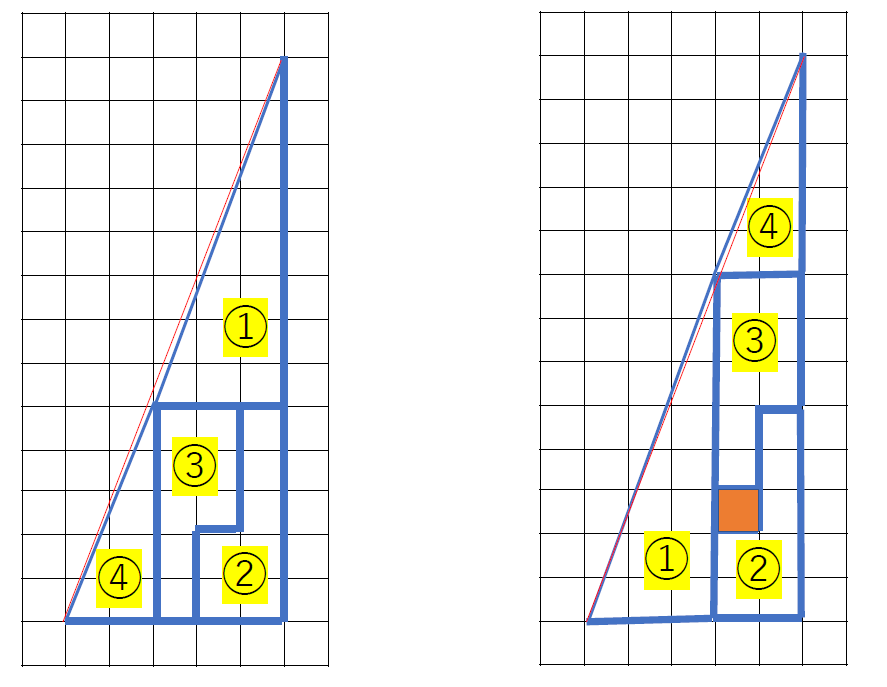
赤色の斜辺の三角形とそれぞれの四角形の面積の差が０．５なのですね。とっさには、変ねと、焦ってしまう問題です。