愛媛の算額－伊佐爾波神社にあるひとつ

MIPO代表の出身地、愛媛県にも算額がいくつも残っており、特に、松山の伊佐爾波神社（いさにわじんじゃ）には、23面も残っているということです。そのうちの一つが、大西佐兵衛の算額というもので、次のようなものです。

伊佐爾波神社の算額
https://isaniwa.official.jp/%e5%be%a1%e5%ae%9d%e7%89%a9/%e7%ae%97%e9%a1%8d/

これは、次のような問題です。
下記の論文（大西佐兵衛と小嶌又兵衛の算額　平田浩一 ・ 河村泰之）より拝借しております。
https://khirata.com/wp-content/uploads/2021/02/160121-ehimesangaku.pdf

この外側の球を、弧環減球と呼ぶそうですが、この弧環減球に、中球２個（直径３寸）と小球１個（直径２寸）を入れたときに残る部分の体積（外積）を求めよというものです。

上記の論文（平田浩一先生、河村泰之先生）を頼りに、少し工夫しながら解いていくことにしました。解き方の方針は、まず、弧環減球の体積を求めます。次に、３つの球の体積を引きます。

そして、弧環減球の体積を求めるには、この元になる球とその外側にある仮想的な大きな球を２次元的に表現して計算します。図で表すと次のような関係です。円1が弧環減球に対応します。外側の円２に対応する球にて、球体が切り取られて弧環減球の形になります。

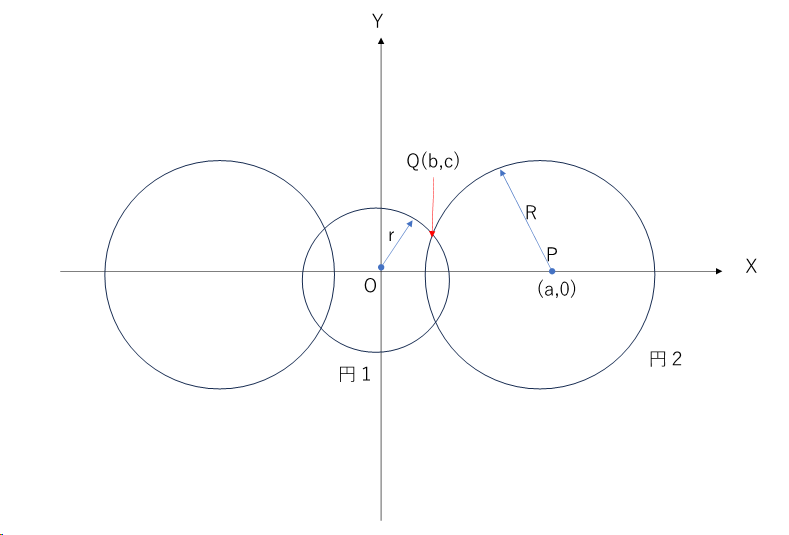
弧環減球の体積をまず、求めることにします。

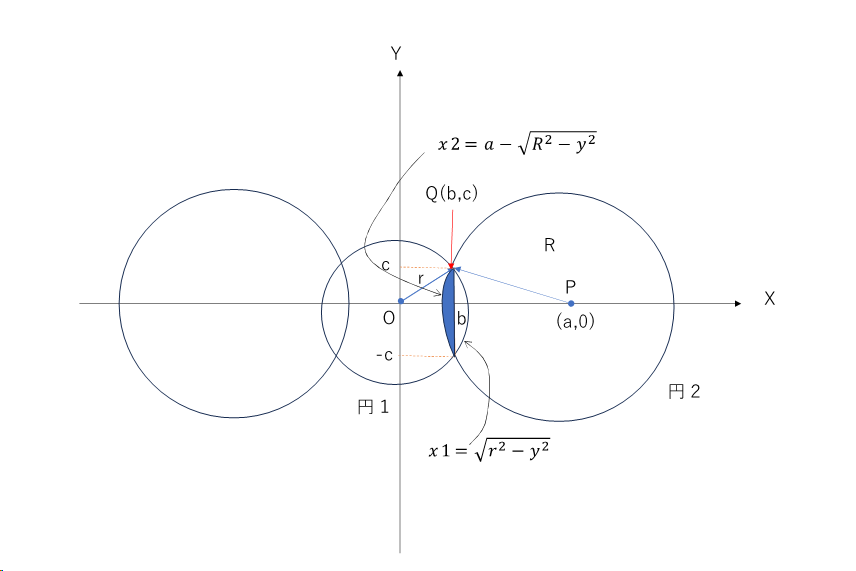
この式で、2つの中球と1つの小球の半径で、ｒ、a、Ｓを表現することで、弧環減球の体積を求めます。それから、2つの中球と1つの小球の体積を引けば、残る部分の体積（外積）が求まります。

この計算は、かなりのボリュームとなるので、次回とします。あ～しんど　(*´з`)　　つづく