フラクタル図形もChatGPTとPythonで描けました(*^-^*)

PythonのプログラムはJupyter Notebook（これにプログラムを書けばイイということをこの間理解しました）に書いて、RUNすると、プログラムが実行します。

その結果、こんなフラクタル図形が描けました。

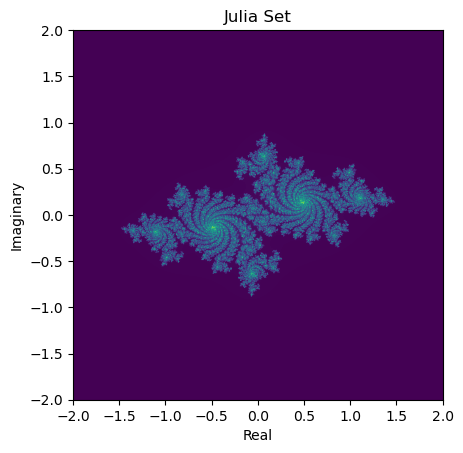
ChatGPTに教えてもらったプログラムは次のものです。

私の指示は、「他のフラクタル図形を描くプログラムを教えてくれますか？」だけです。

ChatGPTの回答は「もちろんです。以下に、別の有名なフラクタル図形であるジュリア集合を描くPythonの例を示します。」ということで、以下のプログラムの提示がありました。

import numpy as np
import matplotlib.pyplot as plt

def julia(z, c, max_iter):
n = 0
while abs(z) <= 2 and n < max_iter:
z = z*z + c
n += 1
return n

def create_julia_image(width, height, x_min, x_max, y_min, y_max, c, max_iter):
image = np.zeros((width, height))

for x in range(width):
    for y in range(height):
        real = x * (x_max - x_min) / (width - 1) + x_min
        imag = y * (y_max - y_min) / (height - 1) + y_min
        z = complex(real, imag)
        color = julia(z, c, max_iter)
        image[x, y] = color

return image

width = 800
height = 800
x_min, x_max = -2.0, 2.0
y_min, y_max = -2.0, 2.0
max_iter = 1000
c = complex(-0.7, 0.27015) # Juliaの定数

julia_image = create_julia_image(width, height, x_min, x_max, y_min, y_max, c, max_iter)

plt.imshow(julia_image.T, extent=(x_min, x_max, y_min, y_max))
plt.title(“Julia Set”)
plt.xlabel(“Real”)
plt.ylabel(“Imaginary”)
plt.show()

何ということですかね～。
ちなみに、c = complex(-0.2, 0.7) # Juliaの定数と変更すると、次のような不細工な絵になりました（笑い）

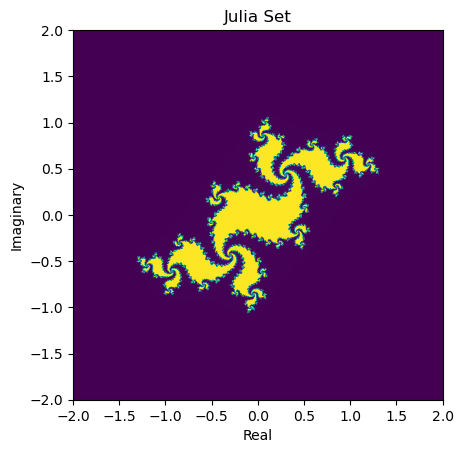
ChatGPTに「ジュリアの定数って何です？」と聞いたら、次のように教えてくれました。

「ジュリア集合を描画する際に、その形状や構造を決定するのが「ジュリアの定数」です。ジュリア集合は複素数の集合であり、その形状はジュリアの定数の値によって異なります。

ジュリア集合は、複素数平面内の点に対して反復的な計算を行い、その点がジュリア集合内にあるかどうかを決定します。この計算には以下の式が使用されます。

zn+1​=zn＾2​+c

ここで、z は複素数、c はジュリアの定数です。zn​ は n 回の反復後の値を示し、その値がある閾値を超えない限り計算は続けられます。

ジュリア集合の外観は、ジュリアの定数 c の値によって異なります。c の値を変えることで、異なるジュリア集合が得られます。異なる c の値によって、フラクタルの形状や複雑さが変化します。」

なるほど！！