Frank Morleyの定理を知ってますか？ーPart2

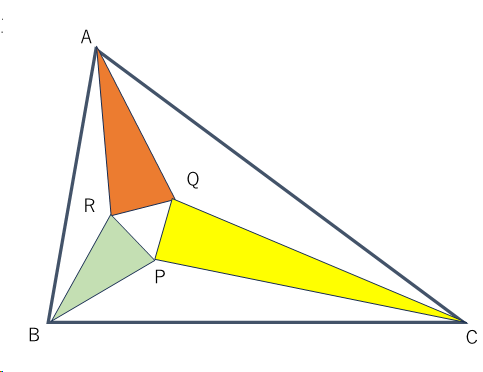
以前（2023年12月9日）に、本サイトに掲載した通り、モーリーの定理とは「任意の三角形において、３つの頂点から引いた角の３等分線（それぞれの頂点から２本ずつ引く）の交点を結ぶと正三角形になる」というものです。ちょうど、下図の三角形PQRは正三角形であるというものです。

そのコラムで一つの解法を掲載しましたが、その末尾に「う～ん、三角関数の式変形が大変です。このほかの解き方もあるようなので、調べてみます。」と記しながら、その他の解き方については放置していました。しかし、最近、次のブログを発見しました（私の投稿から９日後でした）

https://koshix.blogspot.com/2023/12/blog-post_18.html

このKunio Koshigiriさんは、同じ大学で机を並べて勉強したお仲間ですが、大学の先生（教授）にまでなられた方です。その解き方は、次のようなものです。

図形の問題は苦手なので，解析幾何学の手法でできないか考えてみた。

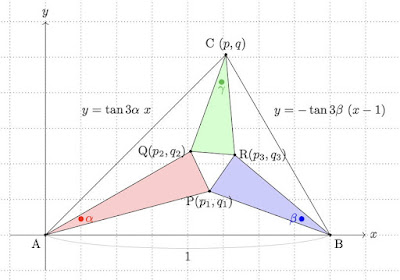
1辺と両端の2角を与えれば三角形は定まる。現れるすべての座標はその辺の長さに比例するので，辺の長さAB=1とする。∠A=3α，∠B=3β，∠C=3γとすると，γ=π/3−α−βで定まる。結局全ての量が２つの角度α,βα,βで表される。

これは実は問題の対称性を損ねるので，標準解答と比較しても良策ではないのだけれど，乗り掛った舟なのでやってみる。

まず三角形ABCの頂点Aを原点(0,0)とし，頂点Bを(1,0)とする。このとき頂点C(p,q)は，y=tan⁡3αとy=−tan3β(x−1)の交点として求まり，(p,q)=(tan3β/(tan3α+tan3β), tan3αtan3β/(tan3α+tan3β))となる。

同様にして，∠の三等分線の交点として(P,Q,R)の3点求めればよい。・・（中略）・・ (p1,q1)=(tanβ/(tanα+tanβ),tanαtanβ(tanα+tanβ)) ・・（中略）・・ (p2,q2)=((ptan(3β+2γ)+q)/(tan2α+tan(3β+2γ)),tan2α{ptan(3β+2γ)+q}/(tan2α+tan(3β+2γ))) ・・（中略）・・ (p3,q3)=((ptan(3β+γ)−tan2β+q)/(tan(3β+γ)−tan2β),−(tan2β{(p−1)tan(3β+γ)+q}/(tan(3β+γ)−tan2β)))

これから3点の距離を計算すれば良いのだけれど，ちょっと人間の手には負えなかった。Mathematicaで計算すると，なんとか確認することができた。　

In[1]:= c[a_, b_] := Pi/3 – a – b

In[2]:= p[a_, b_] := Tan[3 b]/(Tan[3 a] + Tan[3 b]) q[a_, b_] := Tan[3 a] Tan[3 b]/(Tan[3 a] + Tan[3 b]) …（中略）・・・

Out[9]= 0　

うわあ～ムズい！？

ということで、どの分野も、深く、深く知っていれば、別の解が有り得るということですね。
Koshigiri先生どうも有難う！！　変な船に乗せてしまってゴメンナサイ (#^.^#)