MIPO

MANABE INTELLECTUAL PROPERTY OFFICE

2と、 1729と、 87539319と、・・・は何の数？

これらの数は、タクシー数（ｎ番目のタクシー数をTa(n)と書く）というのですって！？　立方数の和に関する数であり、次のWikipedia を参照。

フリー百科事典『ウィキペディア（Wikipedia）』 タクシー数
https://ja.wikipedia.org/wiki/%E3%82%BF%E3%82%AF%E3%82%B7%E3%83%BC%E6%95%B0　

{\displaystyle {\begin{aligned}\operatorname {Ta} (1)=2&=1^{3}+1^{3}\end{aligned}}}
{\displaystyle {\begin{aligned}\operatorname {Ta} (2)=1729&=1^{3}+12^{3}\\&=9^{3}+10^{3}\end{aligned}}}
{\displaystyle {\begin{aligned}\operatorname {Ta} (3)=87539319&=167^{3}+436^{3}\\&=228^{3}+423^{3}\\&=255^{3}+414^{3}\end{aligned}}}
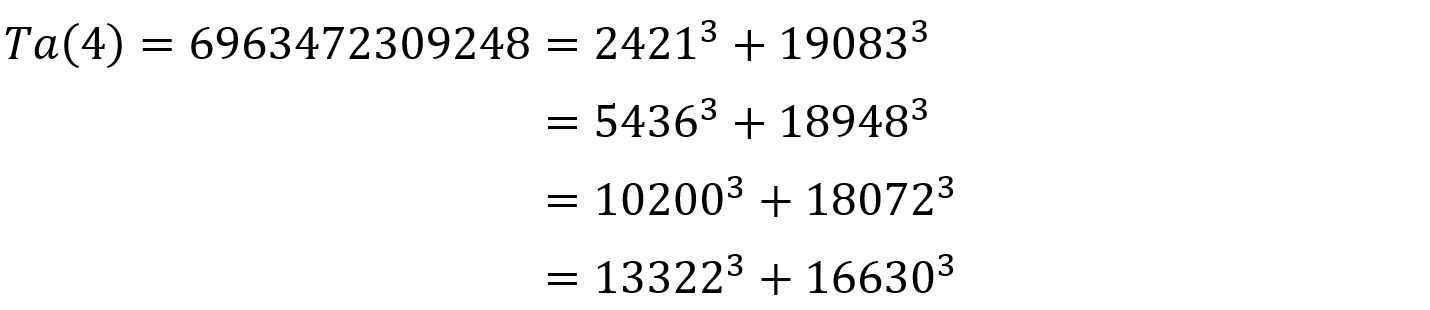
{\displaystyle {\begin{aligned}\operatorname {Ta} (4)=6963472309248&=2421^{3}+19083^{3}\\&=5436^{3}+18948^{3}\\&=10200^{3}+18072^{3}\\&=13322^{3}+16630^{3}\end{aligned}}}
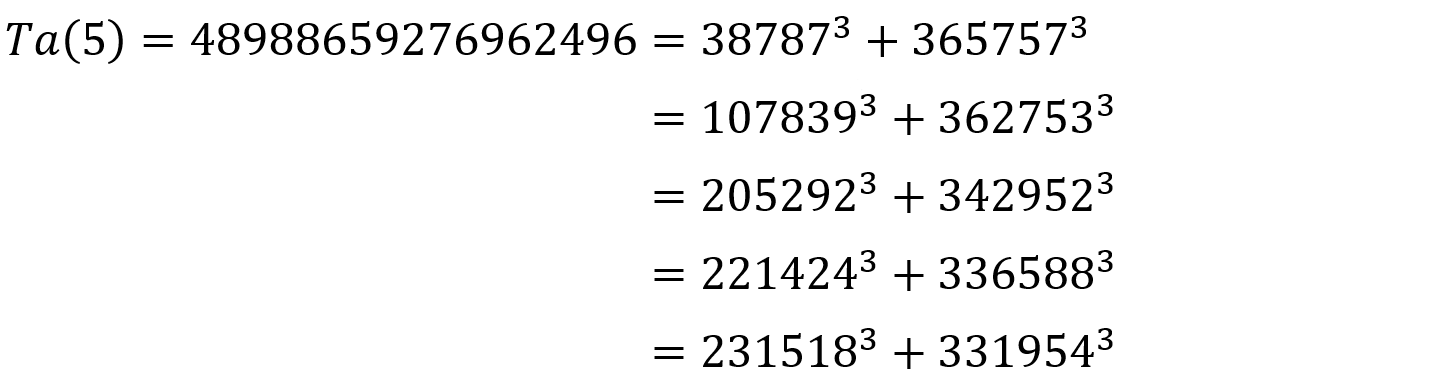
{\displaystyle {\begin{aligned}\operatorname {Ta} (5)=48988659276962496&=38787^{3}+365757^{3}\\&=107839^{3}+362753^{3}\\&=205292^{3}+342952^{3}\\&=221424^{3}+336588^{3}\\&=231518^{3}+331954^{3}\end{aligned}}}
{\displaystyle {\begin{aligned}\operatorname {Ta} (6)=24153319581254312065344&=582162^{3}+28906206^{3}\\&=3064173^{3}+28894803^{3}\\&=8519281^{3}+28657487^{3}\\&=16218068^{3}+27093208^{3}\\&=17492496^{3}+26590452^{3}\\&=18289922^{3}+26224366^{3}\end{aligned}}}

となり、現在まで上記のTa(6)までは、見つけられ証明されているけどTa(7)以上は、候補は見つけられているけど、未だ証明がされていないとか。ヨビノリさんの次のYouTubeで、わかりやすく説明してくれております。

ラマヌジャンの天才エピソードでおなじみ【タクシー数】