安島直円(あじま なおのぶ)という江戸時代中期の和算家が発見した定理に「安島‐マルファッティの定理」というものがあります。これは、三角形に三つの互いに接する円の性質を解き明かしたもので、イタリアの数学者マルファッティ(Malfatti)よりも発見が早かったというものです。
具体的には、次のような三角形(辺の長さが、507,375,252)に内接する3つの円の直径を求めよという問題です。
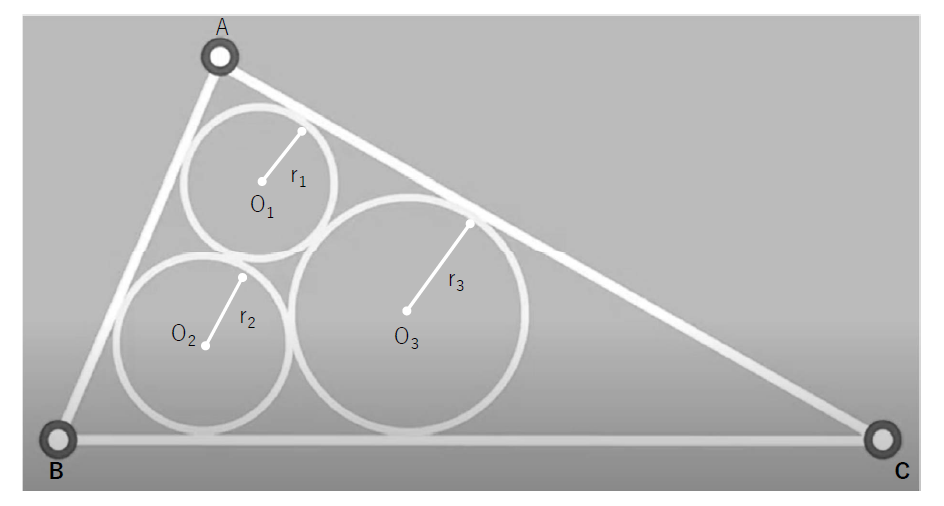
この3つの円のそれぞれ接点を夫々の頂点から延長すると点Iで交差し、この点Iは、実は三角形の内心です。
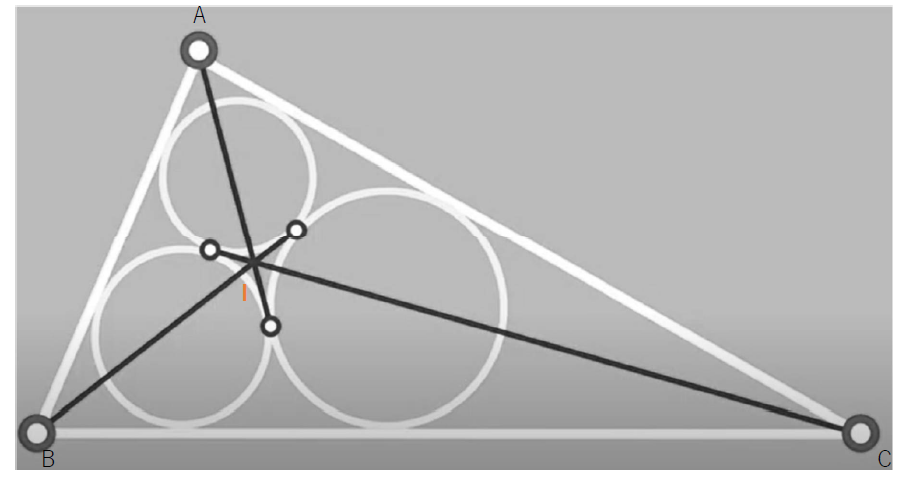
そこで、順を追って計算を進めますが、参考になったものは、次の資料でした。
【1分de幾何学】マルファッティの円
https://www.youtube.com/watch?v=zab7-Z5BKTo
SSH数学図形ゼミ 12.Malfattiの問題(三斜三円術)
http://sshmathgeom.private.coocan.jp/Malfatti%20problem/Malfattiindex.html
さらに細かく検討するために使用したのは、次の手書きの図面です(見にくくてスミマセン)。
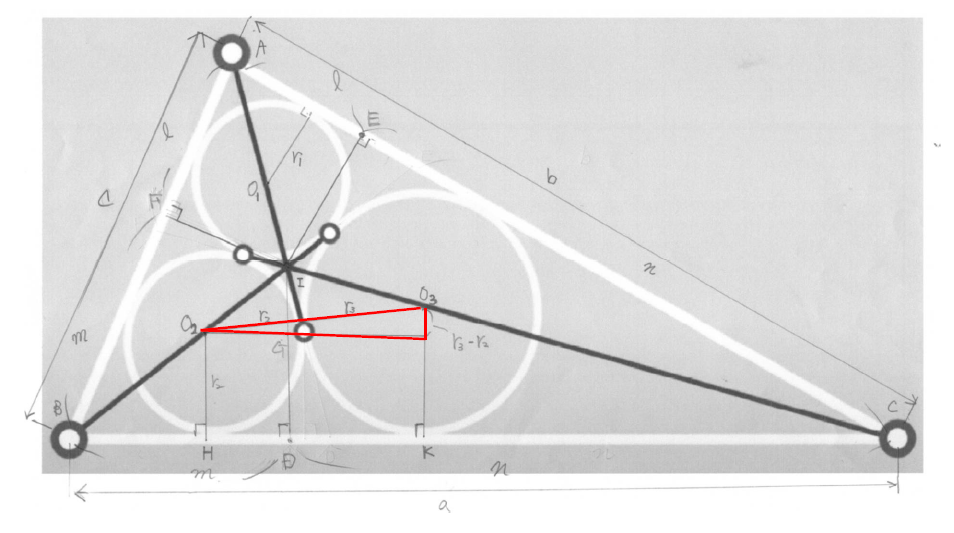
まず、BCの長さをaとし、ACの長さをbとし、ABの長さをcとし、内心IからBCへの垂線をおろした交点をDとし、ACへの垂線をおろした交点をE、ABへの垂線をおろした交点をFとして、AF=AE=ℓ、BD=BF=m、CD=CE=nとすると、a=m+n、b=n+ℓ、c=ℓ+mより、
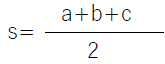
とおくと、m=s-b ・・・①、n=s-c ・・・②、ℓ=s-a ・・・③ が得られます。
また、図の赤色の三角形にピタゴラスの定理を適用すると次式が成立します。
HK2=(r2+r3)2-(r3-r2)2 =4r2r3 となり、次式が成立します。
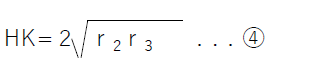
そして、


ここで、式➈に注目すると、2yz=HK=t-ℓ+√(t2+ℓ2)=IE-AE+AI ・・・式⑮ この式⑮の HK=IE-AE+AI が安島・Malfattiの定理とよばれるものであります。
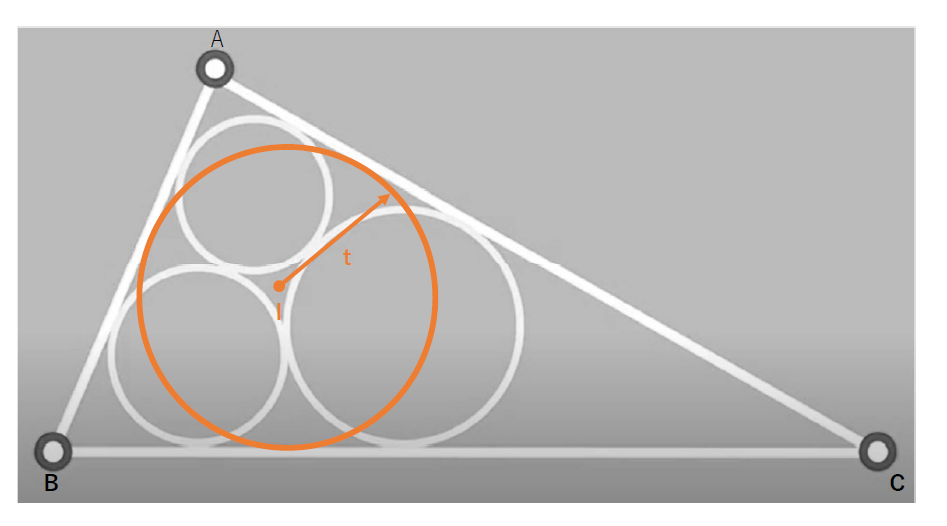
さて、最初の問題の答えを導くことができるようになりました。a=507, b=375, C=252 とした場合、内接円の半径tは、三角形ABCの面積Sを
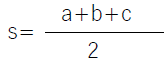
で割れば求まります(t=S/s)。ここで、s=567となります。
三角形ABCの面積Sは、ヘロンの公式から
S=√s(s-a)(s-b)(s-c) =45360となり、内接円の半径t=45360/567=80
また、式➈~⑪を計算して、α=60、β=48、γ=45となり、式⑫~⑭により、r1=36、r2=56.25、r3=64となります。
従って、3つの内接円の直径は、72、112.5、128となります。
しかし、見た目とくらべて、とても大変な問題でした (^-^;