物理の減衰振動もChatGPTは解いてくれますね～

次のグラフは、ChatGPTが描いてくれました。上が位置（ｘ）、下が速度（dx/dt)を示します。

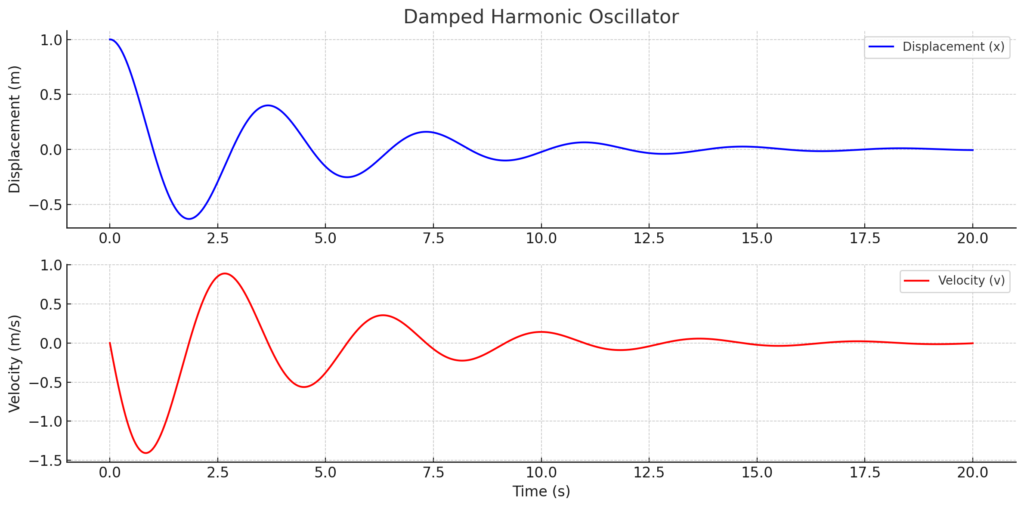
私の問いかけは
「こんばんわ。抵抗がある減衰振動の二階微分方程式を解いて、それをグラフに作りたいのです。描くプログラム（Python）とできるグラフを描いてみることはできますか？　初期値はお任せします。」
これに対して、ChatGPTは、以下の解答をくれました。

Pythonのプログラムを開くと次の通りでした。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

＃Parameters for the damped harmonic oscillator

m = 1.0 # mass (kg)
c = 0.5 # damping coefficient (kg/s)
k = 3.0 # spring constant (N/m)

＃Initial conditions: x0 = initial displacement, v0 = initial velocity

x0 = 1.0 # initial displacement (m)
v0 = 0.0 # initial velocity (m/s)

＃Differential equation for the damped harmonic oscillator

def damped_oscillator(u, t, m, c, k):
x, v = u
dxdt = v
dvdt = -(c/m) * v – (k/m) * x
return [dxdt, dvdt]

＃Time points where the solution is computed

t = np.linspace(0, 20, 1000)

＃Initial conditions vector

u0 = [x0, v0]

＃Solve the differential equation

solution = odeint(damped_oscillator, u0, t, args=(m, c, k))
x = solution[:, 0]
v = solution[:, 1]

＃Plotting the solution

plt.figure(figsize=(12, 6))

＃Displacement (x) over time

plt.subplot(2, 1, 1)
plt.plot(t, x, label=’Displacement (x)’, color=’b’)
plt.title(‘Damped Harmonic Oscillator’)
plt.ylabel(‘Displacement (m)’)
plt.legend()

＃Velocity (v) over time

plt.subplot(2, 1, 2)
plt.plot(t, v, label=’Velocity (v)’, color=’r’)
plt.xlabel(‘Time (s)’)
plt.ylabel(‘Velocity (m/s)’)
plt.legend()

plt.tight_layout()
plt.show()

「このプログラムでは、odeint 関数を使用して微分方程式を数値的に解いています。プログラムの結果として得られたグラフは、減衰振動の変位と速度の時間依存性を示しています。」
とのコメントでした。

ChatGPTは、微分方程式まで数値計算で解いてゆく（プログラムを自動作成する）のですね。驚きです！！　そして、odeint関数は何かと問うたところ、

「odeint関数は、Pythonの科学計算ライブラリであるscipyに含まれる関数の一つで、常微分方程式（Ordinary Differential Equations, ODE）の数値解を求めるために使用されます。特に、初期値問題の形で表されるODEを解くのに適しています。　odeintは、裏側で複雑な数値解法（例えばルンゲ＝クッタ法）を使用しており、多くの種類の微分方程式システムに対して効果的です。特に物理学、工学、生物学などの分野で広く利用されています。」

ということも教えてもらいました。これを使いこなすともっと色々できるんでしょうね。　世の中、進んでる～