2024年大阪大学入試－前期理系数学2－別解

2024年の阪大の入試問題の数学の中でこの第２問が最も難しかったようです。すでに解答をしましたが、この問題には別解があり、そちらの方が解き方としてはしっくりくるかもしれません。

問題は次の通りです。

だいたい複素数α、βが動くってどういうこと！と思いますが、これはいろいろな値をとるということですね。しかし複素数の絶対値とは、例えばa+biの絶対値は、√（a^2+b^2)と思い浮かべると、この大きさを反映とする円周にある、つまりこの複素数a+biは、√（a^2+b^2)・exp(iθ)という表現にかえられることに気づくべきです。ここで、cosθ＝a/√（a^2+b^2) , sinθ＝ｂ/√（a^2+b^2)であります。従って、複素数a+biの絶対値がｒ以下となれば、これは半径ｒの円周内（円周を含む）の範囲で動くことを意味します。

こういった観点で、問題を解くと別解として次のようになります。

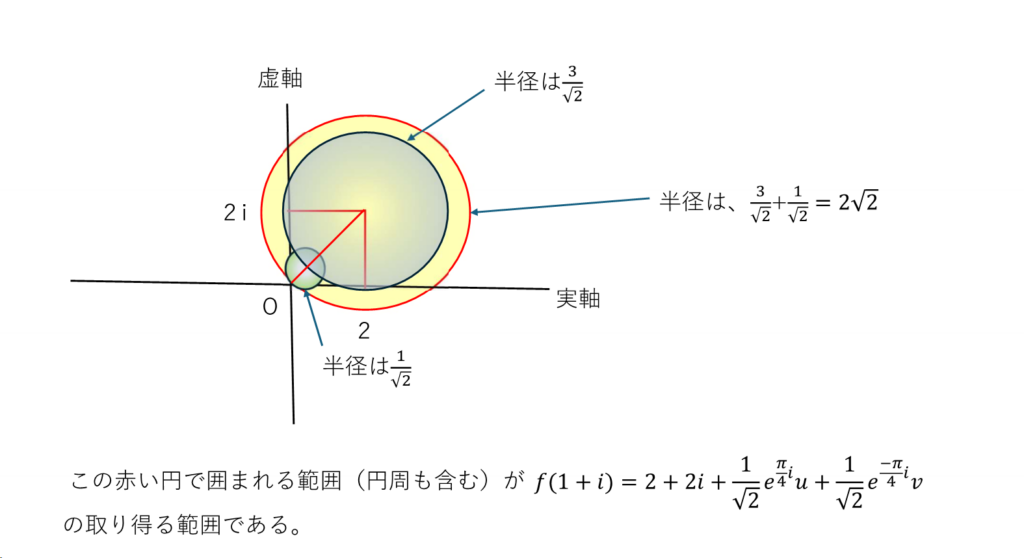
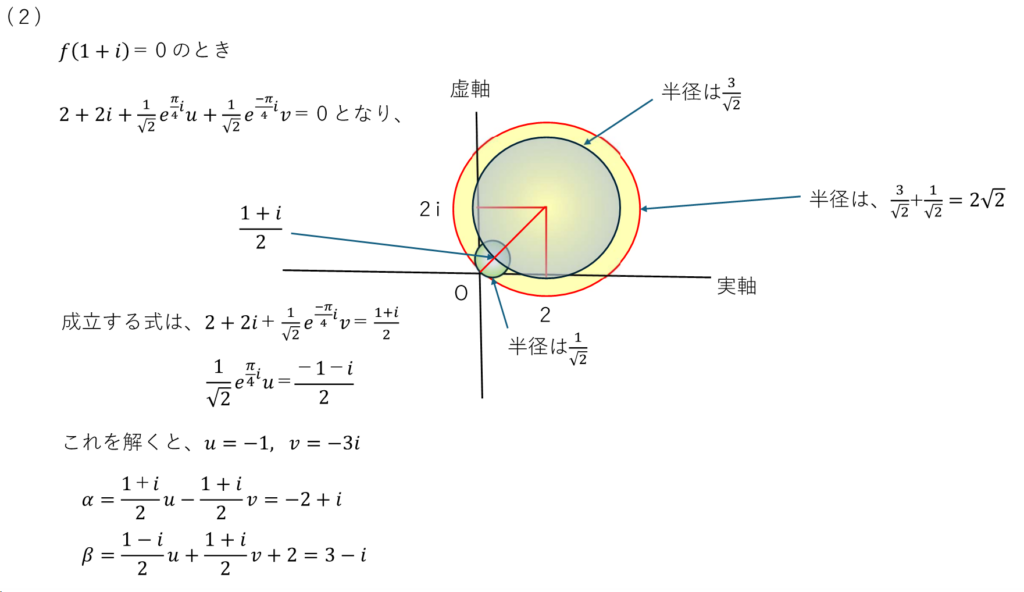
これで、おわりです。今年の阪大の入試問題は難化したと言われています。問題を見て、解き方がさっぱり分からなくとも、ちょっとずつ知恵を出していけば、最終的に解けます。時間があればの話ですが。受験生は大変ですね。さあ、みんながんばろ！